Autocatalysis is essential for the origin of life and chemical evolution. However, the lack of a unified framework so far prevents a systematic study of autocatalysis. Here, we derive, from basic principles, general stoichiometric conditions for catalysis and auto-catalysis in chemical reaction networks. This allows for a classification of minimal autocatalytic motifs called cores. While all known autocatalytic systems indeed contain minimal motifs, the classification also reveals hitherto unidentified motifs. We further examine conditions for kinetic viability of such networks, which depends on the autocatalytic motifs they contain and is notably increased by internal catalytic cycles. Finally, we show how this framework extends the range of conceivable autocatalytic systems, by applying our stoichiometric and kinetic analysis to autocatalysis emerging from coupled compartments. The unified approach to autocatalysis presented in this work lays a foundation toward the building of a systems-level theory of chemical evolution.
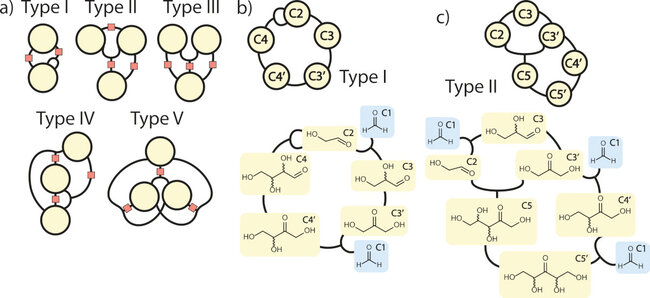
(A) Five minimal motifs. Orange squares indicate where further nodes and reactions may be added, provided this preserves the motif type (I, II, III, IV, V) and minimality. (B and C) Examples of chemical networks, along with their autocatalytic cores. Blue, external species; yellow, autocatalysts. (B) Type I: Breslow’s 1959 mechanism for the formose reaction (32). (C) Type II: Another autocatalytic cycle in the formose reaction. Species denoted as Cx inside the nodes refer to molecules containing x carbon atoms, which are shown below in standard chemical representation.
Reference: Alex Blokhuis, David Lacoste, and Philippe Nghe
PNAS October 13, 2020 117 (41) 25230-25236
doi.org/10.1073/pnas.2013527117

