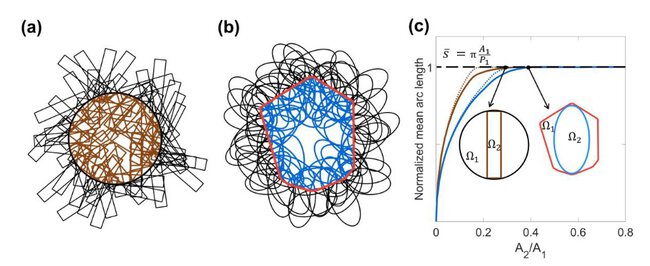
 A remarkable result from integral geometry is Cauchy’s formula, which relates the mean path length of ballistic trajectories randomly crossing a convex 2D domain, to the ratio between the region area and its perimeter. This theorem has been generalized for non-convex domains and extended to the case of Brownian motion to find many applications in various fields including biological locomotion and wave physics. Here, we generalize the theorem to arbitrary closed trajectories exploring arbitrary domains. We demonstrate that, regardless of the complexity of this trajectory, the mean arc length still satisfies Cauchy’s formula provided that no closed trajectory is entirely contained in the domain. Below this threshold, the mean arc length decreases with the size of the closed trajectory. In this case, an approximate analytical formula can still be given for convex closed trajectories intersecting convex domains provided they are small in comparison. To validate our analysis, we performed numerical simulations of different types of trajectories exploring arbitrary 2D domains. Our results could be applied to retrieve geometric information of bounded domains from the mean first entrance-exit length.
A remarkable result from integral geometry is Cauchy’s formula, which relates the mean path length of ballistic trajectories randomly crossing a convex 2D domain, to the ratio between the region area and its perimeter. This theorem has been generalized for non-convex domains and extended to the case of Brownian motion to find many applications in various fields including biological locomotion and wave physics. Here, we generalize the theorem to arbitrary closed trajectories exploring arbitrary domains. We demonstrate that, regardless of the complexity of this trajectory, the mean arc length still satisfies Cauchy’s formula provided that no closed trajectory is entirely contained in the domain. Below this threshold, the mean arc length decreases with the size of the closed trajectory. In this case, an approximate analytical formula can still be given for convex closed trajectories intersecting convex domains provided they are small in comparison. To validate our analysis, we performed numerical simulations of different types of trajectories exploring arbitrary 2D domains. Our results could be applied to retrieve geometric information of bounded domains from the mean first entrance-exit length.
EUROPEAN PHYSICAL JOURNAL PLUS
Volume137
Issue4
Article Number501
By: Hidalgo-Caballero, Samuel; Cassinelli, Alvaro; Labousse, Matthieu; Fort, Emmanuel
Published: APR 2022
DOI10.1140/epjp/s13360-022-02700-z
ArXiv version

