Odd elasticity and topological waves in active surfaces

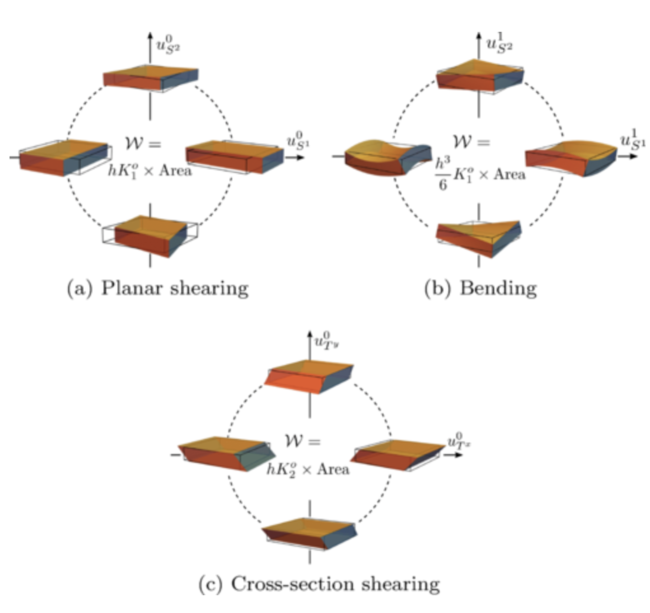
Odd elasticity describes active elastic systems whose stress-strain relationship is not compatible with a potential energy. As the requirement of energy conservation is lifted from linear elasticity, new antisymmetric (odd) components appear in the elastic tensor. In this work we study the odd elasticity and non-Hermitian wave dynamics of active surfaces, specifically plates of moderate thickness. These odd moduli can endow the vibrational modes of the plate with a nonzero topological invariant known as the first Chern number. Within continuum elastic theory, we show that the Chern number is related to the presence of unidirectional shearing waves that are hosted at the plate’s boundary. We show that the existence of these chiral edge waves hinges on a distinctive two-step mechanism. Unlike electronic Chern insulators where the magnetic field at the same time gaps the spectrum and imparts chirality, here the finite thickness of the sample gaps the shear modes, and the odd elasticity makes them chiral.

By: Michele Fossati, Colin Scheibner, Michel Fruchart, and Vincenzo Vitelli
Phys. Rev. E 109, 024608 – Published 28 February 2024
[DOI: https://journals.aps.org/pre/abstra...]