Branching processes with resetting as a model for cell division

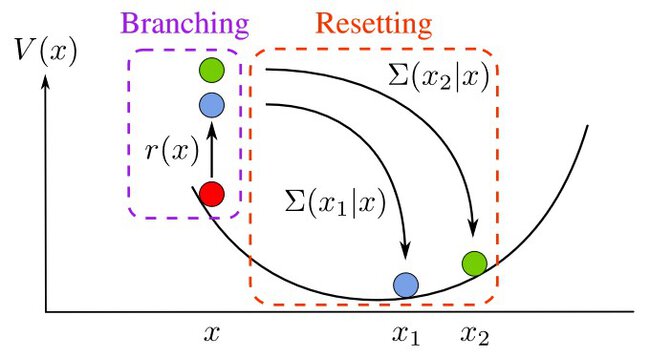
We study the stochastic thermodynamics of cell growth and division using a theoretical framework based on branching processes with resetting. Cell division may be split into two sub-processes: branching, by which a given cell gives birth to an identical copy of itself, and resetting, by which some properties of the daughter cells (such as their size or age) are reset to new values following division. We derive the first and second laws of stochastic thermodynamics for this process, and identify separate contributions due to branching and resetting. We apply our framework to well-known models of cell size control, such as the sizer, the timer, and the adder. We show that the entropy production of resetting is negative and that of branching is positive for these models in the regime of exponential growth of the colony. This property suggests an analogy between our model for cell growth and division and heat engines, and the introduction of a thermodynamic efficiency, which quantifies the conversion of one form of entropy production to another.

JOURNAL OF PHYSICS A-MATHEMATICAL AND THEORETICAL
Volume55
Issue7
Article Number074001
By: Genthon, Arthur; Garcia-Garcia, Reinaldo; Lacoste, David
Published: FEB 2022
DOI10.1088/1751-8121/ac491a
ArXiv version