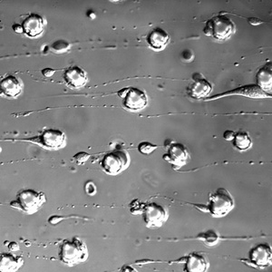
We are theorists and experimentalists working at the interface of physics, chemistry, biology and computer science. Our research focuses on soft matter (colloids, polymers, liquid crystals, granular matter, thin sheets...), active matter (self-propelled colloids, swimming droplets, walking grains, swarms of robots... ) and molecular systems (DNA, RNA, enzymes...). We study various aspects of these systems such as topology, self-assembly, interfaces, information processing, evolution..., while also developing general theoretical methods. The name Gulliver captures the diversity of scales that are studied in the lab.
Discover our Internships and PhD 2024
 Active matter Active Matter
Active matter Active Matter |