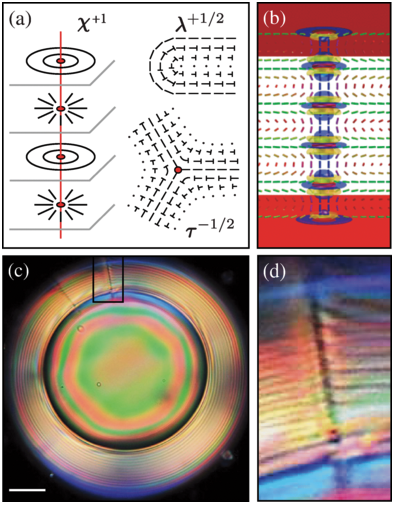
 The Helfrich-Hurault (HH) elastic instability is a well-known mechanism behind patterns that form as a result of strain upon liquid crystal systems with periodic ground states. In the HH model, layered structures undulate and buckle in response to local, geometric incompatibilities in order to maintain the preferred layer spacing. Classic HH systems include cholesteric liquid crystals under electromagnetic field distortions and smectic liquid crystals under mechanical strains, where both materials are confined between rigid substrates. However, richer phenomena are observed when undulation instabilities occur in the presence of deformable interfaces and variable boundary conditions. Understanding how the HH instability is affected by deformable surfaces is imperative for applying the instability to a broader range of materials. In this review, the HH mechanism is reexamined and special focus is given to how the boundary conditions influence the response of lamellar systems to geometrical frustration. Lamellar liquid crystals confined within a spherical shell geometry are used as the model system. Made possible by the relatively recent advances in microfluidics within the past 15 years, liquid crystal shells are composed entirely of fluid interfaces and have boundary conditions that can be dynamically controlled at will. Past and recent work that exemplifies how topological constraints, molecular anchoring conditions, and boundary curvature can trigger the HH mechanism in liquid crystals with periodic ground states is examined. The review ends by identifying similar phenomena across a wide variety of materials, both biological and synthetic. The fact that the HH mechanism is a generic and often overlooked response of periodic materials to geometrical frustration is highlighted.
The Helfrich-Hurault (HH) elastic instability is a well-known mechanism behind patterns that form as a result of strain upon liquid crystal systems with periodic ground states. In the HH model, layered structures undulate and buckle in response to local, geometric incompatibilities in order to maintain the preferred layer spacing. Classic HH systems include cholesteric liquid crystals under electromagnetic field distortions and smectic liquid crystals under mechanical strains, where both materials are confined between rigid substrates. However, richer phenomena are observed when undulation instabilities occur in the presence of deformable interfaces and variable boundary conditions. Understanding how the HH instability is affected by deformable surfaces is imperative for applying the instability to a broader range of materials. In this review, the HH mechanism is reexamined and special focus is given to how the boundary conditions influence the response of lamellar systems to geometrical frustration. Lamellar liquid crystals confined within a spherical shell geometry are used as the model system. Made possible by the relatively recent advances in microfluidics within the past 15 years, liquid crystal shells are composed entirely of fluid interfaces and have boundary conditions that can be dynamically controlled at will. Past and recent work that exemplifies how topological constraints, molecular anchoring conditions, and boundary curvature can trigger the HH mechanism in liquid crystals with periodic ground states is examined. The review ends by identifying similar phenomena across a wide variety of materials, both biological and synthetic. The fact that the HH mechanism is a generic and often overlooked response of periodic materials to geometrical frustration is highlighted.
REV. MODERN PHYSICS
By Christophe Blanc / Guillaume Durey / Randall D. Kamien / Teresa Lopez-Leon / Maxim O. Lavrentovich / Lisa Tran
Rev. Mod. Phys. 95, 015004
DOI: 10.1103/RevModPhys.95.015004

