ESPCI web site
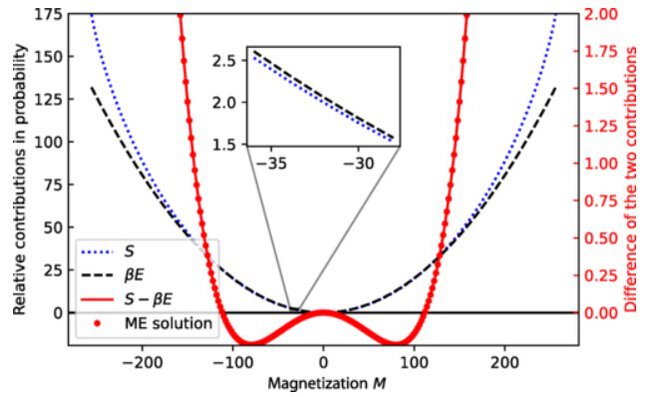
Progressive quenching (PQ) is a stochastic process during which one fixes, one after another, the degrees of freedom of a globally coupled Ising spin system while letting it thermalize through a heat bath. It has previously been shown that during PQ, the mean equilibrium spin value follows a martingale process and this process can characterize the memory of the system. In the present study, we find that the aforementioned martingale implies a local invariance of the path weight for the total quenched magnetization, the Markovian process whose increment is the spin that is fixed last. Consequently, PQ lets the probability distribution for the total quenched magnetization evolve while keeping the Boltzmann-like factor, or a canonical structure, under constraint, which consists of a path-independent potential and a path-counting entropy. Moreover, when the PQ starts from full equilibrium, the probability distribution at each stage of PQ is found to be the limit distribution of what we call recycled quenching, the process in which a randomly chosen quenched spin is unquenched after a single step of PQ. The local invariance is directly derived from the martingale property, and not from other known theorems on martingale processes.
PHYSICAL REVIEW E
Volume: 105 Issue: 4
Article Number: 044146
By: Moslonka, Charles ; Sekimoto, Ken
Published: APR 2022
[DOI10.1103/PhysRevE.105.044146 https://journals.aps.org/pre/abstra...]
[ArXiv version https://arxiv.org/pdf/2106.14821.pdf]