 The motion of a colloidal probe in a complex fluid, such as a micellar solution, is usually described by the generalized Langevin equation, which is linear.
The motion of a colloidal probe in a complex fluid, such as a micellar solution, is usually described by the generalized Langevin equation, which is linear.
However, recent numerical simulations and experiments have shown that this linear model fails when the probe is confined and that the intrinsic dynamics of the probe is actually nonlinear.
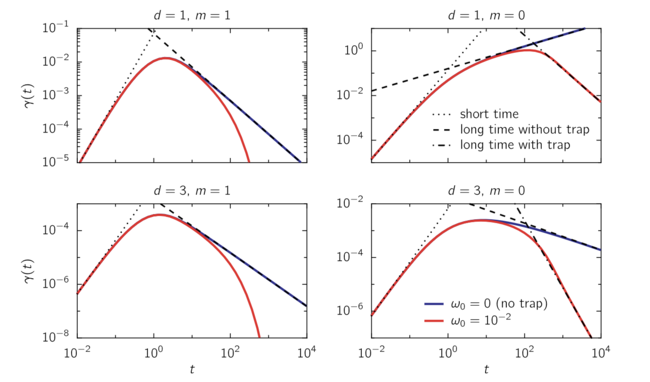
Noting that the kurtosis of the displacement of the probe may reveal the nonlinearity
of its dynamics also in the absence confinement, we compute it for a probe coupled to a Gaussian field and possibly trapped by a harmonic potential. We show that the excess kurtosis increases from zero at short times, reaches a maximum, and then decays algebraically at long times, with an exponent which depends on the spatial dimensionality and on the features and correlations of the dynamics of the field.
Our analytical predictions are confirmed by numerical simulations of the stochastic dynamics of the probe and the field where the latter is represented by a finite number of modes.
PHYSICAL REVIEW E
By: Vincent Démery and Andrea Gambassi.
Phys. Rev. E 108, 044604 – Published 25 October 2023
DOI: https://journals.aps.org/pre/abstra...

